














Of cacti, Martian caves and models of the universe
The search for new worlds beneath the earth
Franke’s greatest scientific achievements are considered to be his cave-theoretical work, including the discovery of the age determination of stalagmites using the C14 method and – building on this – his research on geochronology, which he was able to realize primarily with Mebus Geyh from the Lower Saxony Office for Soil Research. For this work, he has made numerous expeditions, during which he sometimes lived many days underground with research teams in order to be able to penetrate into previously unknown depths.






But to reduce Franke to these cave-scientific works would only cover a small part of his manifold research activities. At this point, therefore, we will present a few other topics that Franke, as a border crosser between science and art, dealt with in the course of his life. They document Franke’s view of scientific questions, which always looked beyond the boundaries of disciplines.
Cacti and the hidden mathematics of Fibonacci numbers




Cacti have been a favorite research object for Herbert W. Franke since the sixties. In his cactus house, he grew numerous of these prickly plants, which not everyone likes, from tiny seeds. Very different aspects fascinated him. First of all, the aesthetics of their forms. The structures of spherical growing cacti belonged to Franke’s special passion, the Krusoni type cacti. Their growth from the inside at the top of the cactus follows the so-called Fibonacci principle, whose fractal mathematics Franke dealt with in depth in the context of his cactus research.




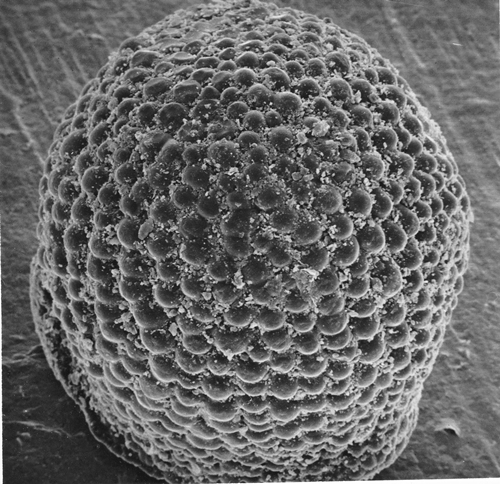
In addition to the Fibonacci numbers and the aesthetics of mathematically describable structures in nature and art, Franke has also thought about the classification criteria of cacti as well as other succulents. In the sixties, for example, the exact determination of houseleeks was only possible during the flowering period. This is because, despite identical leaf shapes, they can differ in terms of species. Franke searched for biophysical alternatives with which succulents and cacti could be identified other than by phenootypical examinations, and here he used a new analytical method from physics. He asked the institute of Dr. Hermann Klingele in Munich to place the seeds of different plants under a scanning electron microscope, SEM for short, the commercial operation of which had only made commercial inroads into analytical technology in the 1960s. The SEM images showed great variability of the seeds and showed the expert that res with the SEM method there was a completely new and, above all, unambiguous possibility of classification–and that even outside the flowering period. The method, which he had already published at that time, soon gained acceptance and is now considered the standard in science for the classification of unknown cactus species.
From Cave Photographer to Generative Artist of Virtual Worlds






Franke began making photographic documentations during his first cave expeditions. The problem with cave photography lies in the illumination of the world in darkness. What began as a hobby quickly developed into professional maturity. Here, too, Franke distinguished himself by the wealth of his indepth knowledge. For example, he used multiple exposure in caves–at that time still with magnesium light–to illuminate especially large cave rooms well for the first time with different light sources. That’s why the people recorded in them often appear somewhat „shadowy.“ They had to keep as still as possible, but that doesn’t always work out perfectly. He quickly developed into a cave photographer whose pictures were readily published in popular magazines as well as in photo journals, usually with altitude reports by the author. Thus, Franke’s writing career as well as his visual art work started deep underground in the caves of Europe. But his pictorial works also began with showing a wet in the light unknown there. However, images with light are not the only way for the physicist to „see“ reality. Thus he experimented already in the fifties not only with light, but for example also with X-rays, in order to show objects, which surround us daily, also „in another light“.
The volcanic caves on Mars and on Big Island of Hawaii






In 1997, on the occasion of a round anniversary of the Association of German Speleologists, the organizer asked Herbert W. Franke if he would like to give the keynote lecture on the history of speleology at the annual meeting. The organizer was thinking of a historical review of cave exploration, which Franke had significantly shaped with numerous expeditions and research results. But Franke had already given so many lectures and written so many books on the subject that he asked if he could also report on something new. Spontaneously it had occurred to him, he could think once about it whether there could be also somewhere outside of the earth–thus on the planets of the solar system–caves. This question had not been raised by the planet research at all up to now. It was interested by the methods of the remote sensing by probes and planet Orbiter up to now exclusively in the pure surface structures of planets. Unfortunately for Franke, it quickly became apparent that limestone mountains on other planets were unknown. But Franke remembered that there is a second type of caves on Earth, the so-called lava caves, which are of volcanic origin.


Thus, Franke looked in the direction of Mars, where the volcano Olympus Mons can come up with a superlative: At a height of 22 kilometers, it is the highest known volcano in the planetary system. All around it lie huge lava fields–and it is precisely in these, Franke thought, that there must be extensive cave spaces, just as on Earth. Lava caves are formed like this: After the eruption, the lava flows off and forms a field of layers around the volcano. When lava production ends, the lava begins to cool and solidify on the outside, while the deeper layers still retain heat, allowing the lava to flow underground. Finally, when the supply of lava stops, the last remnants run off, leaving the underground beds of lava drains as tube-like cavities.
Franke presented his thoughts as a keynote speaker at the conference. And Franke would not be Franke if he had not combined his caves on Mars with a view of the future. The occurrence of caves on Mars, he said, would also have great practical significance: If astronauts landed on Mars, they could live in the caves protected from cosmic radiation–and Franke added at the time that, because of the low gravity on Mars, astronauts could also be protected from muscle decay by exercising in them. In the large caves, for example, it would be possible to set up ping-pong tables! Among the visitors of the conference was also the best connoisseur of volcanic caves: Stephan Kempe, professor of geology at the University of Darmstadt. He came forward immediately after the lecture and remarked that he almost regretted not having come up with the idea himself to deal with the question of lava caves on foreign planets. As great as Kempe’s praise was, so great was the criticism of several other experts concerning the existence of caves on Mars. A few years later there was the „official“ confirmation: NASA delivered the first proof in black and white. On some photos from orbit, not only the black openings of the shaft caves were visible on the surface of Mars, but even parts of the side walls were recognizable.
Incidentally, the intensive examination of Mars and its caves not only inspired Franke to visit the lava cave world in Hawaii in 2004. Mars also became the setting for his novel Escape to Mars, which was published by dtv in 2007.
Alternative universes with world models of Cellular Automaton
In the nineties, Cellular Automaton were an extensive field in which Franke dealt with world models, the formation of structure in the cosmos and also the question of whether the universe in which we live is determined or whether chance also plays a role. Franke used Cellular Automaton for this purpose.
Historical text by Herbert W. Franke on the ZKM exhibition Wanderer between the worlds (2010)
From a modern point of view, the question of what holds the world together is directed to the laws of nature. Already the fact that these can be formulated mathematically gives food for thought, because this is by no means self-evident, but it also offers points of reference for physicists and philosophers in their considerations about world models. This situation is aggravated by an experience which the development of physics has brought with it: At first, it was an increasing number of formulas that were needed to describe what was happening in physics, but over time it emerged that in all disciplines there are more general formulations from which laws that previously seemed independent can be derived, so that less and less descriptive effort was needed for an overview. And already since Einstein’s theory of relativity one played with the idea of a world formula, in which the whole physics can be summarized. However, difficulties arise with such attempts–apparently essential points of view are missing in the proposals offered so far.
An indication of the sense in which an extension might be necessary is provided by computer science. One can formulate it as a principle: Our world behaves as if it were programmed with certain objectives. I have explained it in detail in my book P-Principle (P for ‚program‘) dedicated to these core questions: The fictitious task behind it would be to let a world emerge which is ‚creative‘, so to speak, i.e. has the ability to develop and to produce something new again and again. And also for the kind of the solution there would be a regulation: In view of the experience of the physicists, the program should be as simple as possible. This sounds rather abstract, but we know a way to visualize the situation; it comes in the form of the so-called Cellular Automaton. The best known is the so-called Game of Life by John H. Conway. Imagine a distribution of pieces on a chessboard! There are several of them, distinguished by states, which can be colors or ratios, for example. The game proceeds in steps, which are expressed by the change of positions or also by the addition or also disappearance of game pieces. And most importantly, this gradual evolution follows rules by which each new distribution of tiles is determined by the previous distribution.
These processes suggest an analogy to the structure of our world: The chessboard represents the space, the game pieces function as elementary particles appearing in it and acting on each other and the rules of the game take over the task of the laws of nature. This simulation is closer to reality than it first appears, it corresponds to the views of classical physics. First of all, it is a causal world in which any change is clearly determined by the existing situation. By the way, this game world is quantized, and one can also imagine it running on an unlimited grid surface. Is now with the planar scheme of the life game really already the simplest kind of the representation found? The physicist and mathematician Stephen Wolfram indeed discovered an even simpler possibility, namely the one-dimensional Cellular Automaton, in which the world is accommodated in one line. Wolfram’s idea also offers the advantage that in one image one can not only see a snapshot, but–with image sequences or even animations–the whole development.
The amount of scientific processes that can be investigated with Cellular Automata is immense. Particularly well growth processes, diffusion and corrosion, pattern formation and the like can be captured, and here the interesting possibility emerges to replace mathematical relations, for the capture of which one needs higher mathematics, by components of the game, embodied by certain kinds of Cellular Automata and the associated rules. Here only one example is to be picked out more near, whereby it concerns principle property of the universe. As they have been described so far, cellular automata behave causally, and this property was also attributed to our world until the beginning of the last century. Modern physics, on the other hand, introduced randomness into the ideas we have specifically about nanoscale interactions. The transition from causal to chance-influenced cellular automata is straightforward. I myself have introduced random influences into the programs for various cellular world models. So these are not random changes of structures or law, but selectively acting perturbations as in the well-known quantum jumps of our reality. A more exact analysis leads to the surprising result that only in randomly influenced worlds new structures can form again and again.
The example of the Cellular Automaton thus shows that there must be something like a balance between order and chance, if the world coming into being is to be constant. A preponderance of order, as it is enforced by laws, leads to solidification, which means an end as well as the opposite: If the influence of chance gets out of hand, the world sinks into a disordered movement and thus into chaos–a state, which was called ‚heat death‘ at that time.
Perhaps the real secret of our world lies in the right relationship between the two opposing factors. This situation is reminiscent of the fact that the balanced relationship between order and chance is also supposed to be decisive for the value of a work of art. If this is true, then art can indeed be conceived as something like a reflection of our world. HWF
Last, but not least: Why playing table tennis is actually impossible and yet it works!


In the sixties, Franke, a passionate table tennis player, came across the question of how it is possible for the table tennis player to play this sport at all in connection with his perceptual-psychological reflections on art. For in fact, the light ball flies back and forth at extremely high speeds of up to 180 km/h during butterfly shots. It was thus clear that the reaction speed of the human brain, which was determined neurophysiologically for the first time at that time, was not at all sufficient to calculate the trajectory from the observed initial curve at such a short distance, and to plan a targeted response to a stroke of the opponent from it. Franke was fascinated by this – his question: Why is it possible for a skilled player to react in a targeted manner even though he cannot think fast enough for this from a perceptual-psychological point of view? In doing so, he also relied on the latest knife findings of the Chair of Photogrammetry and Cartography at the Technical University of Braunschweig–and came to the conclusion that the good player already „anticipates“ the trajectory through the body and bat posture of the opponent–i.e. before the latter even executes the stroke. From this anticipation, he can calculate the trajectory and reaction requirement in time.
Under the title Training of Anticipation–Biological Foundations of Table Tennis, Franke published an article on this subject in an issue of the German Medical Journal of the year 1969 with psychological and neuronal research results. It says: The table tennis game moves at the limit of the human reaction capacity and trains „anticipation“–reacting to the intention and not to the action of the opponent.
