















Complex Numbers Series (1980-1995)
Calculating with imaginary quantities – that’s what mathematicians do when they operate with negative roots, which do not exist in classical number theory. But the conventional calculation rules also apply to this type of numbers. Such numbers were still an impossibility for classical mathematicians, but theoretical considerations about such imaginary quantities began as early as the 16th century. Today, number theorists only see the well-known numbers as a special case of complex numbers, in which the minus root is excluded. In the Complex Numbers series, Herbert W. Franke and Horst Helbig moved into this mysterious world of imaginary sizes and uncovered an almost unimaginable variety of aesthetically exciting visualizations.
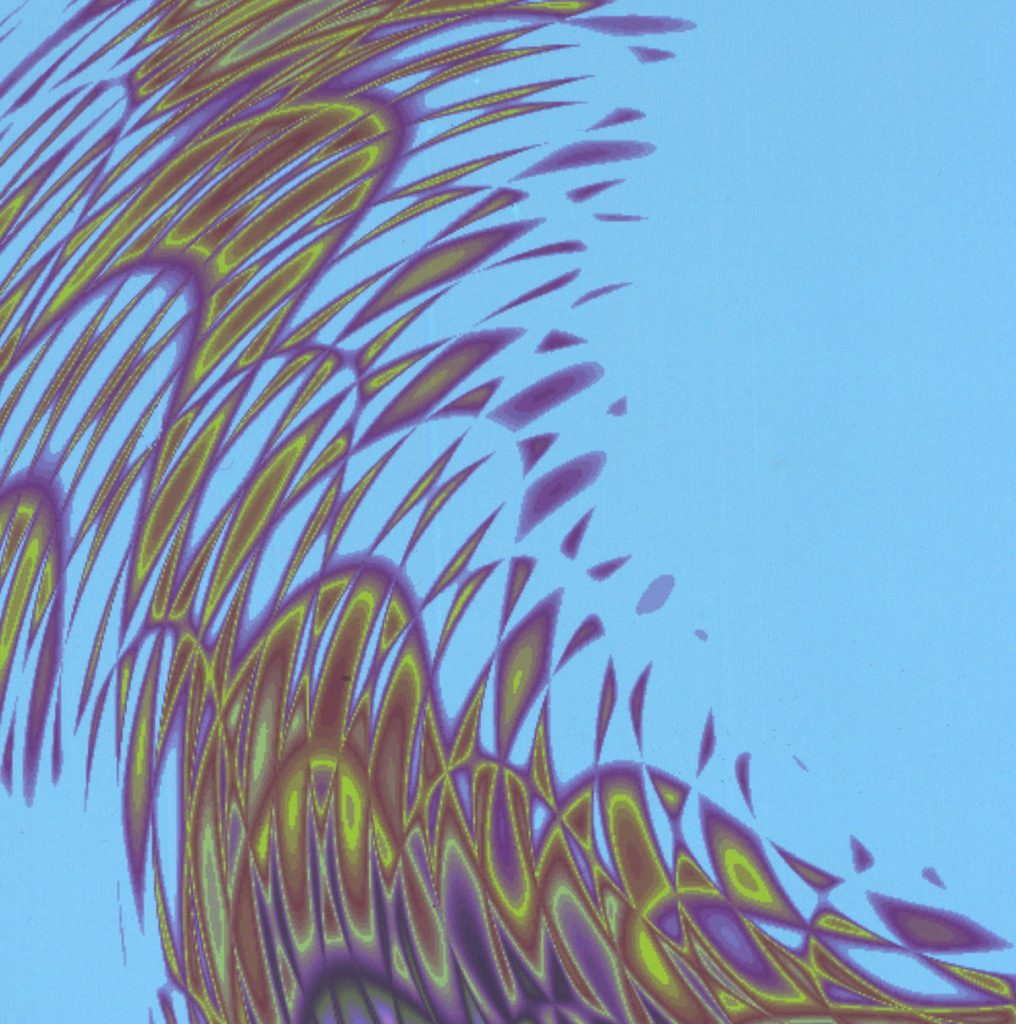



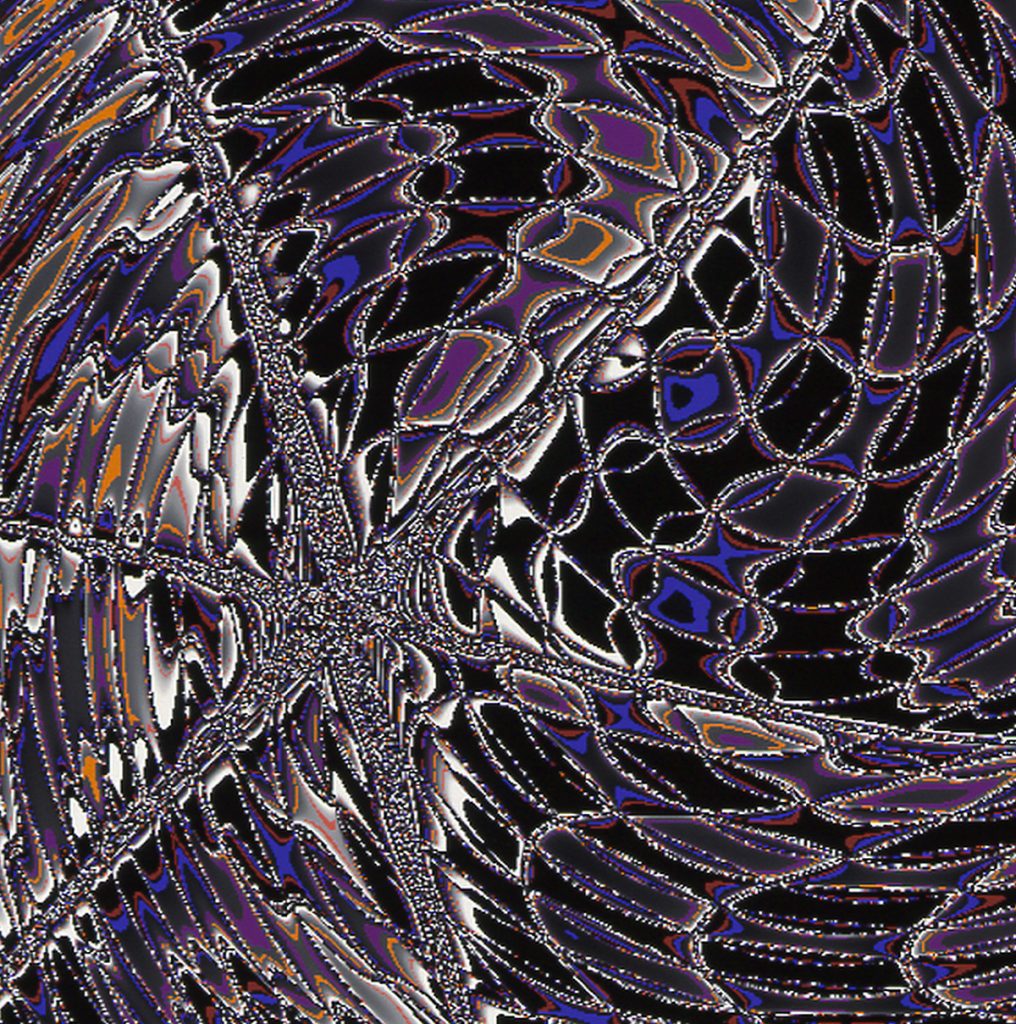

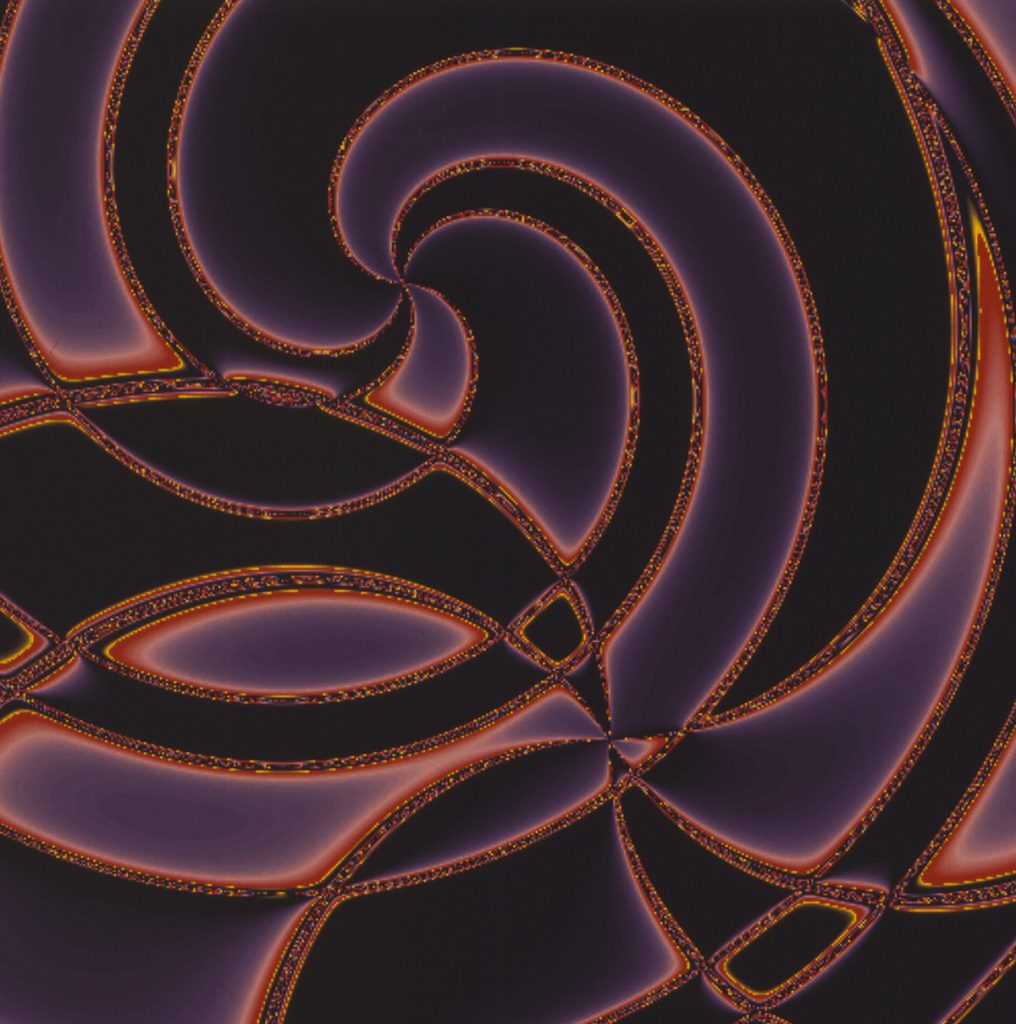

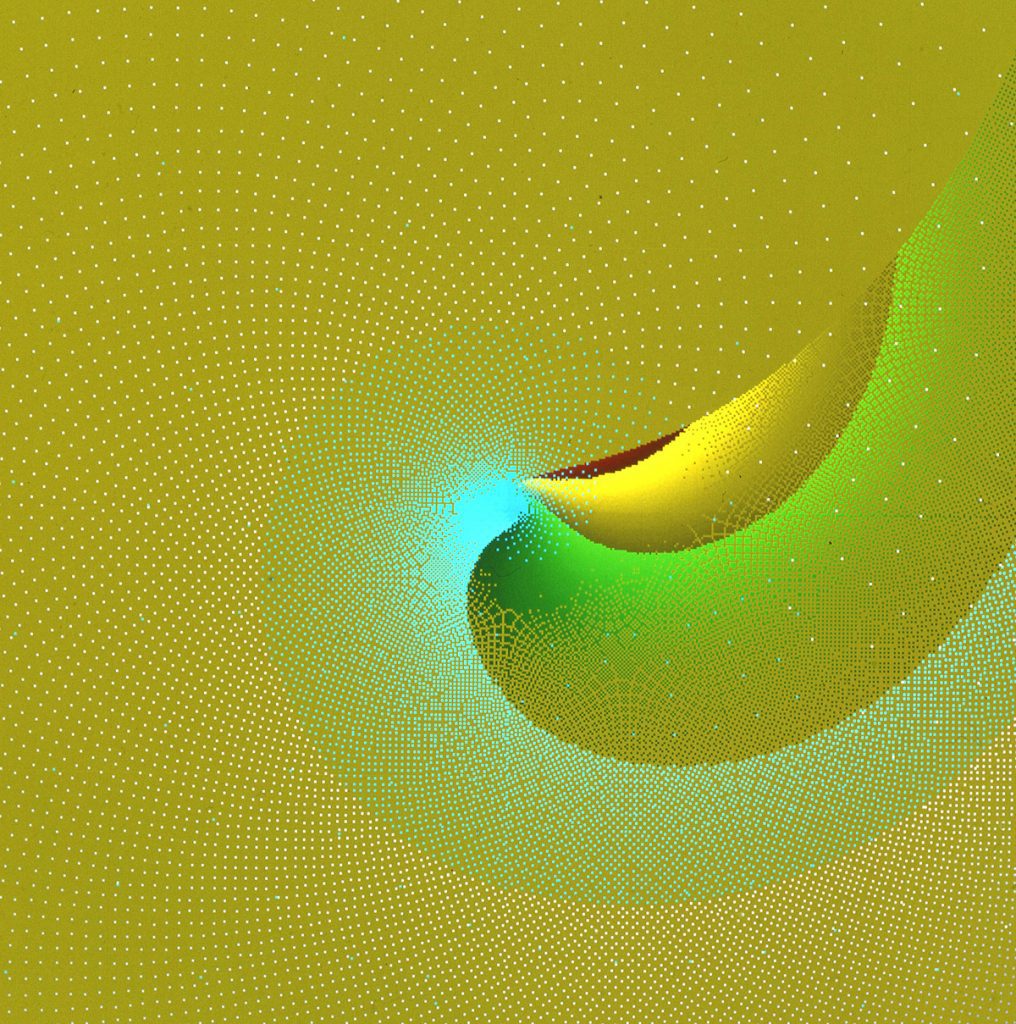





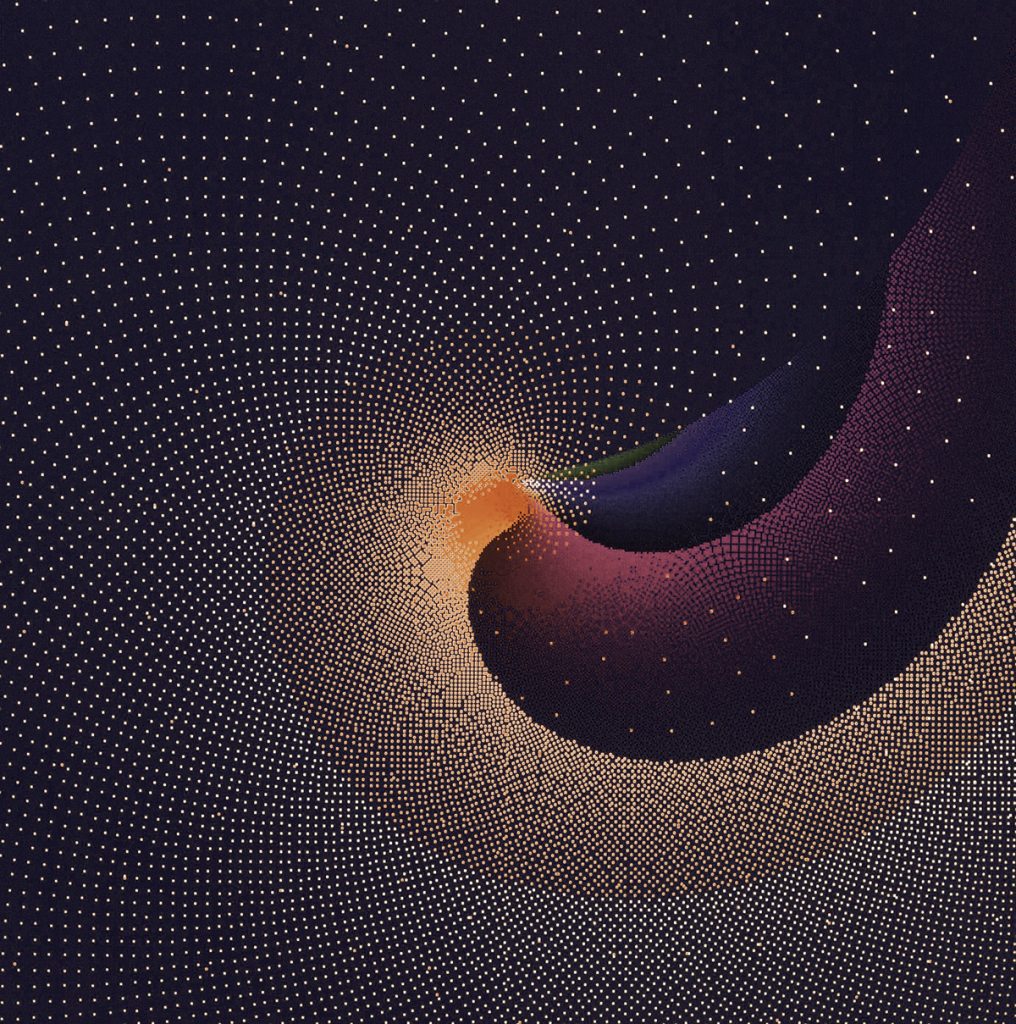

The term Math Art summarizes the results of a long series of experiments that Herbert W. Franke carried out together with the physicist and programmer Horst Helbig from 1980 onwards. It was about the use of mathematical methods, which were not developed and used for scientific purposes, but for aesthetic purposes. The main goal of the 15-year project (1980-1995) was the investigation of numerous mathematical disciplines regarding their aesthetic dimension and the visualization of complex mathematical relationships from algebraic formulas to stochastic relationships. In the course of the work, not only was the aesthetic dimension of formulas and functions explored, but a whole series of new graphic routines were also created, which were integrated into the software DIBIAS (for digital image evaluation system) as a fixed component, including representations in 2D and 3D as well as further processing with the methods of image transformation (picture processing). The heart of the computer was a Comtal Image Processing System and software DIBIAS with a resolution of up to 2048 x 2048 pixels and around 16 million colors.
Hier geht es zu den anderen Serien von Math Art:
Serie Algebra
Serie Buchstaben
Serie Bühnenbilder
Serie Felder
Serie Fourier-Transformationen
Serie Fraktale
Serie Logik
Serie Picture Processing
Serie Zufall
