











Serie Fourier-Transformationen (1980-1995)
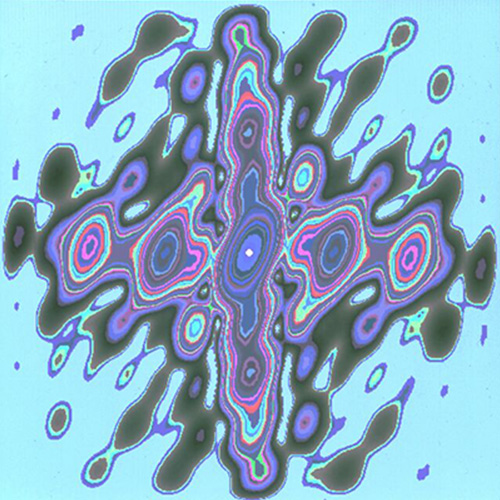
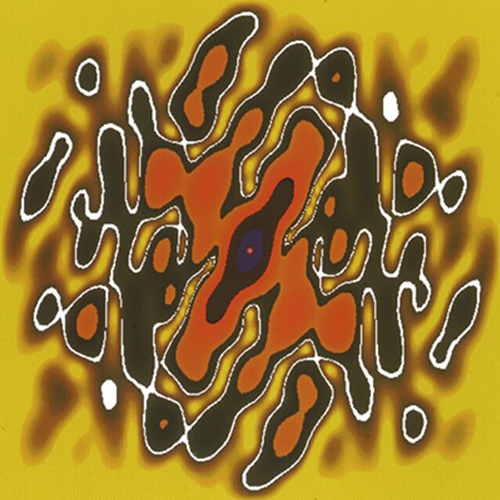
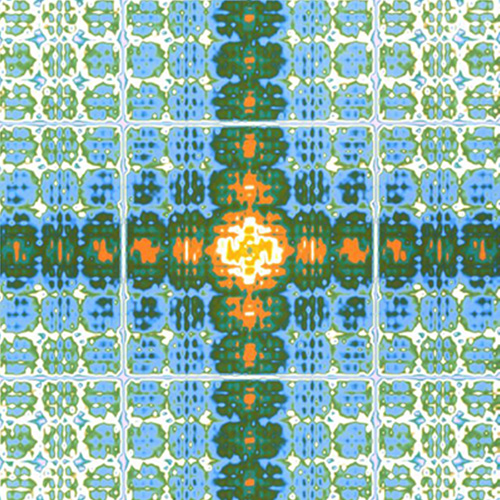
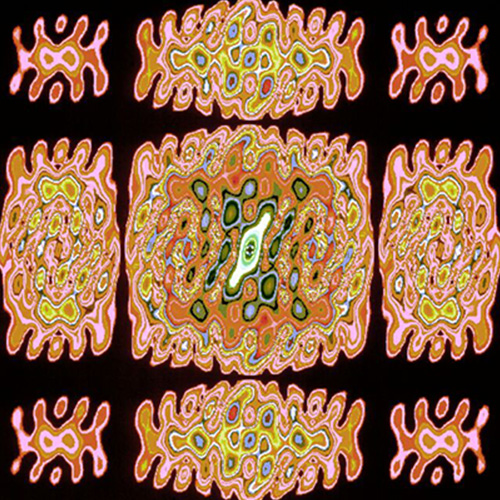
Die Bildserie Fourier-Transformationen entstand im Rahmen der Forschungen zur Math Art von Herbert W. Franke gemeinsam mit dem Physiker und Programmierer Horst Helbig am Deutschen Zentrum für Luft- und Raumfahrt in Oberpfaffenhofen. Fourier-Transformationen basieren auf mathematischen Prinzipien, die bereits im 19. Jahrhundert theoretisch entwickelt worden waren und die heute in der Nachrichtentechnik von großer Bedeutung sind. Sie werden in der digitalen Datenauswertung für die Signalverbesserung und zur Rauschunterdrückung eingesetzt: von Satellitensignalen wie bis zur Medizin, ebenso für die Datenkompression, beispielsweise für das Streaming von TV-Daten im Internet oder für die Telekommunikation. Mit der Serie Fourier-Transformationen hat Franke mit Helbig die mathematischen Prinzipien der Fourieranalyse für zahlreiche künstlerische Experimente eingesetzt. Dabei entstehen typische ornamentale Strukturen mit Symmetrien und Symmetriebrüchen, die fein ziseliert oder auch flächig-integral sein können. Mit solchen Fourier-Transformationen wurde übrigens auch die Serie Buchstaben realisiert.









Mit dem Begriff Math Art werden die Resultate einer langjährigen Versuchsreihe zusammengefasst, die Herbert W. Franke ab 1980 gemeinsam mit dem Physiker und Programmierer Horst Helbig durchgeführt hat. Dabei ging es um den Einsatz mathematischer Methoden, die aber nicht für wissenschaftliche, sondern für ästhetische Zwecke entwickelt und benutzt wurden. Das Hauptziel des insgesamt 15 Jahre währenden Projektes (1980-1995) war die Untersuchung zahlreicher mathematischer Disziplinen im Hinblick auf ihre ästhetische Dimension und die Visualisierung komplexer mathematischer Zusammenhänge von algebraischen Formeln bis zu stochastischen Zusammenhängen. Im Laufe der Arbeiten wurde nicht nur die ästhetische Dimension von Formeln und Funktionen ausgelotet, sondern es entstand dabei auch eine ganze Reihe neuer graphischer Routinen, die der Software DIBIAS (für Digitales Bildauswertungssystem) als fester Bestandteil eingegliedert wurden, darunter Darstellungen in 2D und 3D sowie die Weiterverarbeitung mit den Methoden der Bildtransformation (picture processing). Das Herzstück des Concurrent-Computers von Perkin-Elmer 32/52 war ein Comtal Image Processing System und Software DIBIAS (Digitales Bildauswertesystem) mit einer Auflösung bis zu 2048 x 2048 Pixeln und ca. 16 Millionen Farben.
Hier geht es zu den anderen Serien von Math Art:
Serie Algebra
Serie Buchstaben
Serie Bühnenbilder
Serie Felder
Serie Fraktale
Serie Komplexe Zahlen
Serie Logik
Serie Picture Processing
Serie Zufall
